독립 변숫값을 변형시켜 가면서 함수의 최솟값을 갖도록 하는 독립변수를 구하는 방법인 경사하강법을 배우다.
1. 경사하강법 정의

MSE를 구하는 2 번째 방법인 경사하강법을 배우겠다. 사용할 모델은 sklearn.linear_model의 SGDRegression모델을 사용할 것이다. 경사하강법은 똑같이 MSE가 최소가 되게 하는 최적의 w(기울기)와 b(절편) 값을 찾는 방법이다. 기계가 스스로 학습한다는 딥러닝의 개념이 있게 하는 핵심 알고리즘이다. 원리는 우리가 시각화했던 그래프를 보면 MSE가 최솟값으로 가야 한다. 그럼 접선의 기울기가 0이 되어야 하기 때문에 기울기가 작아지는 쪽으로 계속 이동하여 값을 최적화하는 방법이다. 기울기가 양수이거나 음수인 건 상관이 없다. 그냥 절댓값이 0에 가까울수록 좋은 것이다. 결론은 1차 미분계수를 이용해서 함수의 최소값을 찾아가는 방법이다. 그렇다면 고등수학을 좀 한 사람의 생각은 "그냥 함수의 미분계수가 0인 지점을 구하면 되는 거 아님?"이라는 날로 먹으려는 생각을 하기마련이다. 실제 분석에서 만나게 되는 함수들은 닫힌 형태가 아니거나 형태가 복잡해서 미분계수와 그 근을 계산하기 어려운 경우가 많다. 실제 미분계수를 구하는 과정을 컴퓨터로 구현하는 것에 비해, 경사하강법은 컴퓨터로 쉽게 구현할 수 있다.
결론 : 경사하강법은 x가 커질수록 함수값이 커지면(기울기는 양수 +) x를 음의 방향으로 움직여야 하고, 반대로 x가 커질 수 록 함수값이 작아지면 (기울기는 음수 -) x를 양의 방향으로 옮기면 된다.
2. 경사하강법 주의사항
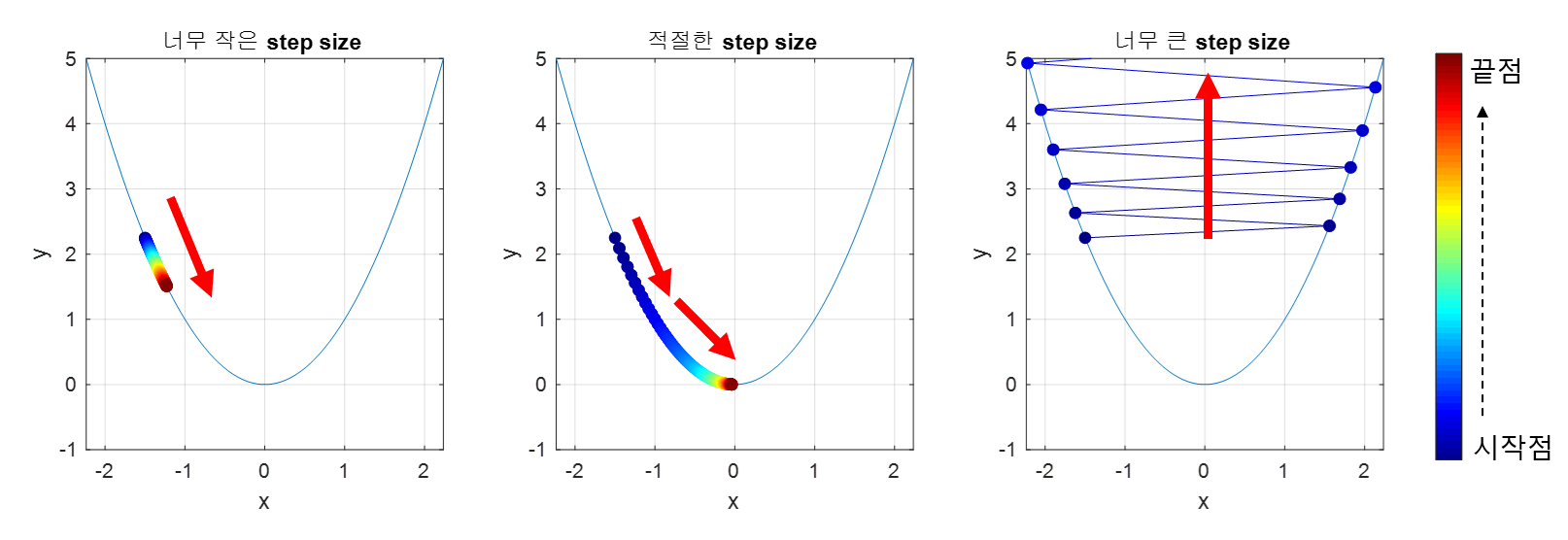
step size는 학습률과 같다. 학습률이 너무 작으면 최솟값을 찾는데 까지 조금씩 움직이기 때문에 시간이 오래걸린다. 그렇다고 학습률이 너무 크면 함수값이 발산하는 현상을 보인다. 발산해버리면 최솟값을 절대 찾지 못할 것이다. 따라서 적절한, 적당한 학습률이 필요하다.

또 학습률이 작으면 Local minima에 빠져서 전체 함수의 최솟값이 아닌 임의의 범위안의 가장 작은 값인 국소값에 빠져버릴 수 있다. Local minima는 전체중에 가장 작은 값이 아닌 임의의 범위 내의 가장 작은 값으로 생각하면 된다. Global minimum은 함수의 최솟값, 즉 전체 범위의 가장 작은값이다. 우리가 찾아야하는 건 Global minimum(빨간 점)이기 때문에 Local minima를 피해야 한다.
'머신러닝' 카테고리의 다른 글
| [머신러닝] 선형회귀 (2) | 2023.09.04 |
|---|---|
| [머신러닝] 특성 선택 (0) | 2023.08.29 |
| [머신러닝] 교차검증 (cross_val_score) (0) | 2023.08.28 |
| [머신러닝] 알고리즘 시각화 (graphviz) (0) | 2023.08.25 |
| [머신러닝] 결정 트리 버섯데이터 실습 (One-hot 인코딩) (0) | 2023.08.25 |
